Drggboy's Blog
0%

有限差分法 实验报告

发表于 更新于

实验题目

利用有限差分法求解

真解为：

要求如下：

  1. 用 sparse 命令组装有限差分矩阵 A。
  2. 算出区间 [-1,1] [-1,1] 分段数为 [5，10，20，40，80，160] 下的数值解及误差，画出数值解图像，并给出误差分析。

实现算法：

有限差分法

程序代码：

建立 model_data.m 文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
function model = model_data(l, r)
% MODEL_DATA 模型数据
% 
% Input
% -----
%  l: 区间左端点
%  r: 区间右端点
%%
% 
%  PREFORMATTED
% 
%  PREFORMATTED
%  TEXT
% 
%  TEXT
% 
 
L = l;
R = r;
%%
% 
%  PREFORMATTED
%  TEXT
% 
 
model = struct('init_mesh', @init_mesh, 'solution', @solution,...
    'source', @source);
 
function [X, h] = init_mesh(NS)
    X = linspace(L, R,NS+1)';
    h = (R - L)/NS;
end
 
function u = solution(x)
%     u=sin(4*pi*x);
        u=(1-x.^2).*exp(-(x.^2));           %真值函数
end
 
function f = source(x)
%     f=16*pi*pi*sin(4*pi*x);
        f=(1-x.^2).*exp(-(x.^2))-exp(-(x.^2)).*(14*(x.^2)-4*(x.^4)-4);   %等式右端函数
end
 
end

建立 FDld_bvp.m 文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
function [uh, x] = FD1d_bvp(model, NS)
%*************************************************************
%% FD1d_bvp 利用中心差分格式求解两点边值问题.
%
% Input
% -----
%   model : 模型数据
%   NS    ：网格剖分段数
% Output
% ------
%   uh ：列向量，长度为 NS+1， 解向量
%   x  : 列向量，长度为 NS+1， 网格节点
%      
 
[x, h] = model.init_mesh(NS);
NV = NS + 1;
 
 %
 %  创建线性差分方程组系数矩阵
 %
 
c1 = -1/h/h;
c2 = 2/h/h;
g = [c1*ones(1, NV-2), 0];
c = [0, c1*ones(1, NV-2)];
d = [1, c2*ones(1, NV-2)+1, 1];
A = diag(g, -1) + diag(d) + diag(c,1);
A = sparse(A);
 
%
%  创建线性差分方程组右端项
%
 
rhs = model.source(x);
rhs(1) = model.solution(x(1));
rhs(end) = model.solution(x(end));
 
%
%  求解上述代数系统.
%
 
uh = A \ rhs;
end

建立 FD1d_bvp_test.m 文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
function [uh, x] = FD1d_bvp(model, NS)
%*************************************************************
%% FD1d_bvp 利用中心差分格式求解两点边值问题.
%
% Input
% -----
%   model : 模型数据
%   NS    ：网格剖分段数
% Output
% ------
%   uh ：列向量，长度为 NS+1， 解向量
%   x  : 列向量，长度为 NS+1， 网格节点
%      
 
[x, h] = model.init_mesh(NS);
NV = NS + 1;
 
 %
 %  创建线性差分方程组系数矩阵
 %
 
c1 = -1/h/h;
c2 = 2/h/h;
g = [c1*ones(1, NV-2), 0];
c = [0, c1*ones(1, NV-2)];
d = [1, c2*ones(1, NV-2)+1, 1];
A = diag(g, -1) + diag(d) + diag(c,1);
A = sparse(A);
 
%
%  创建线性差分方程组右端项
%
 
rhs = model.source(x);
rhs(1) = model.solution(x(1));
rhs(end) = model.solution(x(end));
 
%
%  求解上述代数系统.
%
 
uh = A \ rhs;
end

建立 FD1d_error.m 文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function [e0, e1, emax] = FD1d_error(solution, uh, X)
NN = length(X);
h = (X(end) - X(1))/(NN -1);
u = solution(X);
ee= u - uh;
 
e0 = h*sum(ee.^2);
e1 = sum((ee(2:end)-ee(1:end-1)).^2)/h;
e1 = e1+e0;
 
e0 = sqrt(e0);          %三种不同误差项
e1 = sqrt(e1);
emax=max(abs(ee));
 
end

实验结果与分析：

拟合图像：

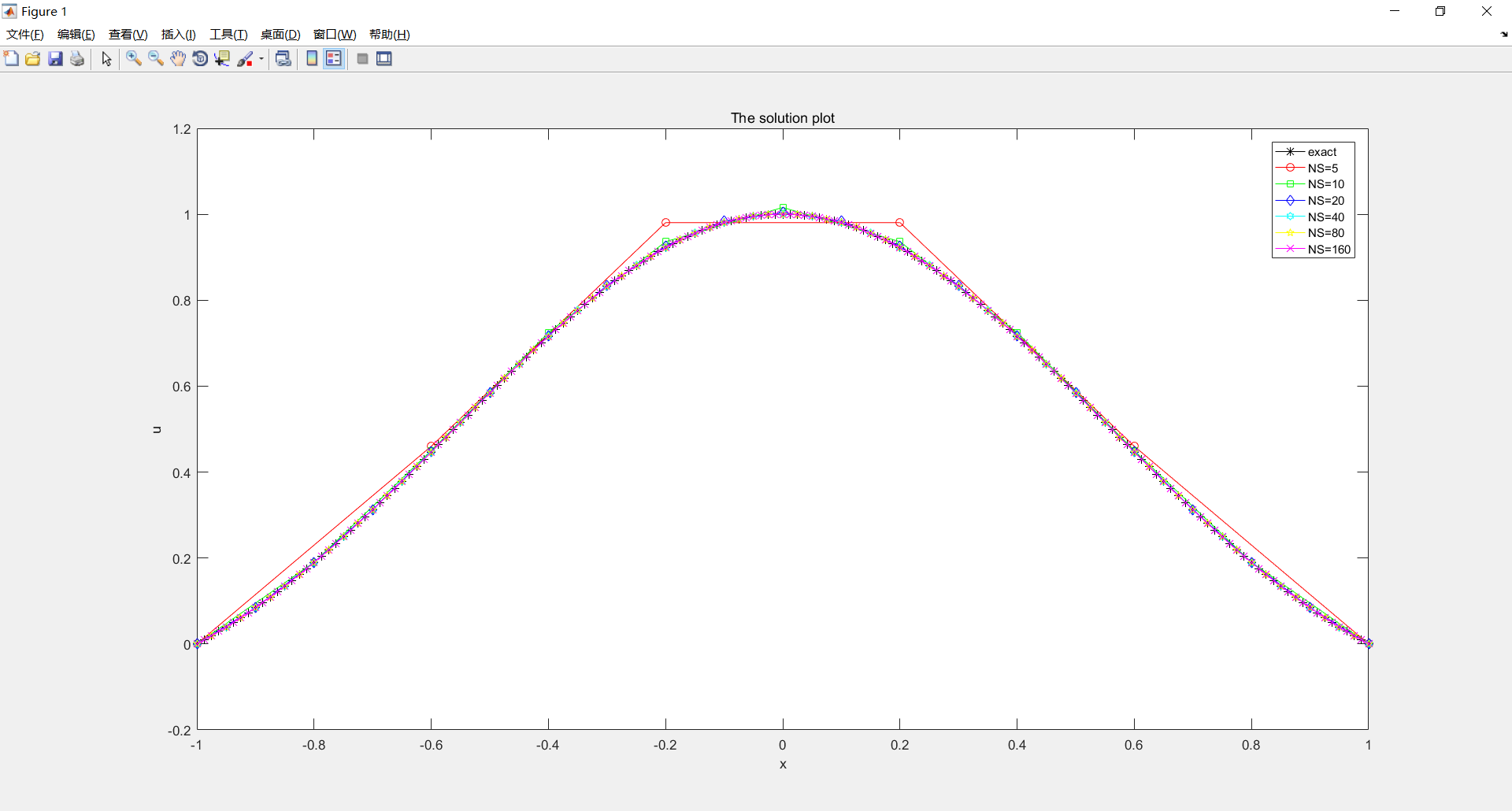
拟合图像

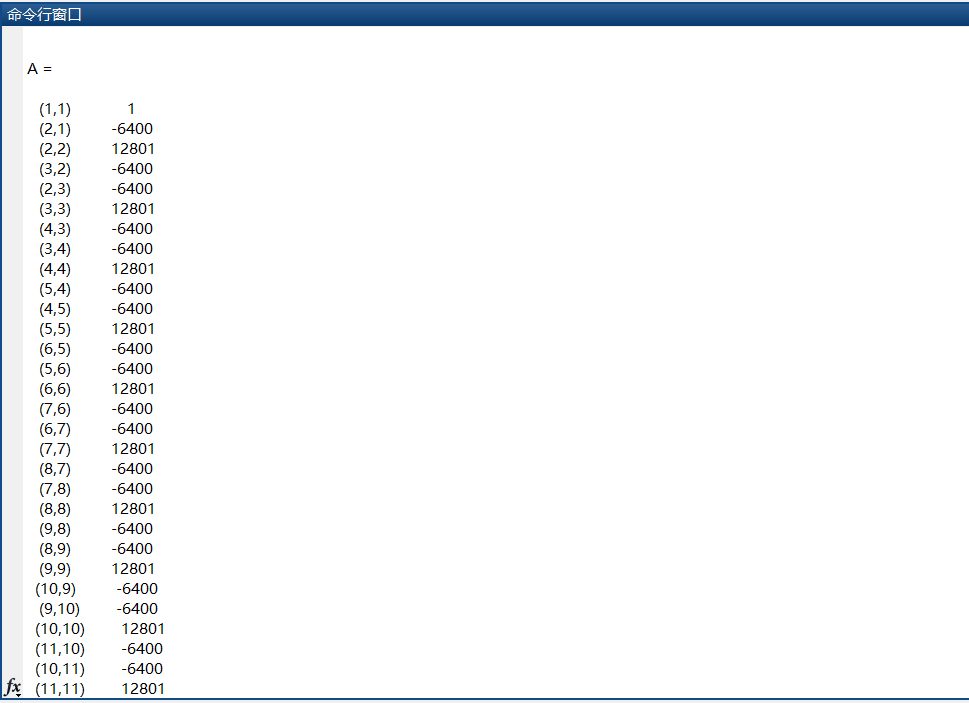
稀疏矩阵A部分项：

稀疏矩阵A

误差项:

误差项

结果分析：

　　随着网格剖分段数的不断增多，画出的图像越来越接近于真值图像，误差也越来越小，根据有限差分方法，当剖分段数不断增多，h趋向于零时，解向量收敛于真值向量。